A Capitalização dos rendimentos: a 8ª Maravilha do mundo, o poder temporal da multiplicação, a magia das finanças e a regra de 72
A 8ª maravilha do mundo segundo Albert Einstein
A capitalização tem um enorme poder exponencial temporal da multiplicação de capitais
A Regra de 72 e o número de anos para duplicar o capital
A capitalização é mágica para investimentos … mas implosiva para dívidas
Principais implicações da capitalização: pagar dívidas e investir o mais cedo possível
A 8ª maravilha do mundo segundo Albert Einstein
Albert Einstein terá uma vez dito que: “a capitalização dos rendimentos é a 8ª maravilha do mundo; aquele que a compreende, ganha-a, aquele que não a entende, paga-a (“The eighth wonder of the world”. “He who understands it, earns it; he who doesn’t, pays it.”)
O que é a capitalização de rendimentos ou o que são rendimentos ou juros compostos?
O capital investido produz rendimento. Esse rendimento pode ser reinvestido conjuntamente com o capital. Ao rendimento produzido pelo investimento do rendimento chama-se capitalização. Capitalização, pois o rendimento do capital torna-se capital para investimento, produzindo ele próprio rendimento.
Também chamado de composição de rendimento (seja de juros, dividendos, etc.). É o ciclo de reprodução do capital, tal como o ciclo de reprodução animal ou das plantas, em que a cria se torna criação.
Sucede que, como iremos ver, a capitalização tem um poder exponencial de multiplicação do capital inicial investido com a passagem do tempo. Por isso, Einstein chamava-lhe a 8ª maravilha ou a magia das finanças a este enorme poder temporal da multiplicação.
A capitalização tem um enorme poder exponencial temporal da multiplicação de capitais
A tabela seguinte mostra o efeito de capitalização tomando como exemplo um capital inicial investido de 100,000 a diversas taxas de rendibilidade anuais entre 2% e 12% por um período até 50 anos (essas taxas de rendibilidade podem ser provenientes de rendimentos periódicos, seja de juros, de dividendos ou mais-valias):

É perfeitamente visível o enorme poder temporal da capitalização. Ao fim de 10 anos, o capital valorizou-se em mais de 2,5 vezes a uma taxa de rendibilidade anual de 10% atingindo 259,374. No final de 20 anos, a essa taxa anual, o capital acumulado seria superior a 670,000 e ao fim de 45 anos excederia 7,2 milhões.
Mesmo para taxas de rendibilidade inferiores o efeito da capitalização é muito significativo. Para uma taxa de rendibilidade de 6%, ao fim de 10 anos o capital já seria de 179,085, ultrapassaria os 320,000 aos 20 anos e seria de 1,37 milhões ao fim de 45 anos.
Estes períodos e estas taxas de rendibilidade são realistas e admissíveis, não sendo, por isso, exagerados. O prazo da nossa poupança para a reforma excede os 45 anos que é a nossa vida ativa normal, 20 anos é um horizonte para a educação universitária dos filhos e 10 anos pode corresponder ao período para a compra (entrada) de uma casa ou o lançamento de um negócio próprio.
Vimos no artigo sobre as taxas de rendibilidade médias anuais dos principais ativos que no período desde 1926 até hoje para os EUA, 12% foi o valor registado pelas ações das pequenas empresas e 5% pelo das obrigações do tesouro a 10 anos. Vimos ainda no mesmo artigo que as taxas de rendibilidade anuais históricas para ações e obrigações não eram muito diferentes destes valores.
O gráfico seguinte mostra o efeito de capitalização para um mesmo capital inicial de 100,000 e para valores de taxas de rendibilidade anuais entre 2% e até 10% por um prazo até 40 anos:

O efeito multiplicativo exponencial é perfeitamente visível no gráfico.
A Regra de 72 e o número de anos para duplicar o capital
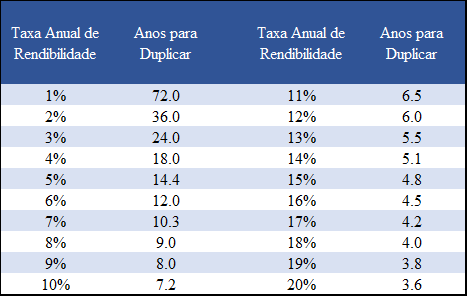
A “Regra de 72” é uma regra simples ou de polegar, muito útil para se obter o número de anos necessários para duplicar o capital para cada valor de taxa de rendimento. Essa regra dá-nos uma boa aproximação para calcularmos rapidamente o número de anos necessários para duplicarmos o capital:
Dividindo 72 por o valor da taxa de rendibilidade anual obtém-se o prazo (em anos) para duplicarmos o capital

Exemplos: 72 / 3% = 24 anos; 72 / 6% = 12 anos; 72 / 12% = 6 anos; etc.
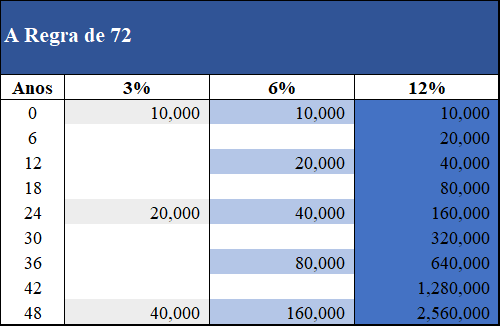
Se passarmos para valores:
Com 10.000 a 3% => 20.000 (24 anos); => 40.000 (48 anos);
Com 10.000 a 12% => 20.000 (6 anos); => 40.000 (12 anos); => 160.000 (24 anos) => 2.560.000 (48 anos)!
Compound Interest Calculator | Investor.gov
A capitalização é mágica para investimentos … mas implosiva para dívidas
A Capitalização é válida para aplicações ou investimentos, mas também para dívidas ou empréstimos, pois aplica-se sempre que há fluxos periódicos, seja de rendimentos ou seja custos.
Para as aplicações ou investimentos temos uma capitalização positiva. Os rendimentos multiplicam-se. Funciona como a “magia da reprodução”. É o “Sonic The Hedgehog” (o saltitão) nas finanças. Estão sempre a soprar ventos favoráveis que nos empurram para a frente.
Mas para as dívidas ou empréstimos temos o inverso, uma capitalização negativa. Os custos multiplicam-se. Funciona como a “a espiral da degeneração”. O “Pacman” (o comilão) nas finanças. Estão sempre a soprar ventos contrários que nos puxam para baixo.
A capitalização é simultaneamente a maravilha e o monstro (“the beauty and the beast”)
Principais implicações da capitalização: pagar dívidas e investir o mais cedo possível
Sendo o fator multiplicativo ou geométrico, e não aritmético, o efeito da capitalização torna-se exponencial.
Por isso, devemos viver sem dívidas. Se as mesmas forem necessárias (educação, saúde, etc.), devemos pagá-las quanto antes.
Por isso, devemos também reaplicar os rendimentos das aplicações e investimentos.
Quanto mais cedo se começar a investir melhor. Por pouco que seja. Qualquer pequeno atraso no presente, significa um maior esforço no futuro.