Le rendement composé est la 8ème merveille du monde, la croissance forte du temps, la magie financière et la règle des 72
La 8ème merveille du monde selon Albert Einstein
Le rendement composé a un énorme potentiel exponentiel pour la croissance du capital avec le temps
La règle des 72 et le nombre d’années pour doubler la capitale
Le rendement composé est magique pour les investissements … mais implosif pour les dettes
Principales implications du rendement composé: payer les dettes et investir dès que possible
La 8ème merveille du monde selon Albert Einstein
Albert Einstein a dit un jour: “Le rendement composé est la huitième merveille de la monde; Celui qui le comprend le gagne; Celui qui ne le fait pas le paye. “
Qu’est-ce qui compose le revenu ou les intérêts?
Le capital investi produit un revenu. Ce revenu peut être réinvesti conjointement avec la capitale. Le revenu généré par le revenu de réinvestissement est appelé capitalisation. Rendement composé, puisque le revenu du capital devient un capital d’investissement, se produisant des revenus.
Il est également appelé composition du revenu (intérêts, dividendes, etc.). C’est le cycle de reproduction de la capitale, tel que le cycle de reproduction animale ou les plantes, dans lequel la progéniture devient créateur.
Comme nous le verrons, le rendement composé a un pouvoir exponentiel pour multiplier les capital initial investi avec le temps. Einstein a appelé la 8ème merveille du monde ou la magie de la finance à cet énorme pouvoir de croissance du capital de temps.
Le rendement composé a un énorme pouvoir exponentiel pour le capital croissance avec le temps
Le tableau suivant montre l’effet du rendement composé en prenant comme exemple une capital initial investi de 100 000 euros et plusieurs taux de rendement annuels, entre 2% et 12%, pour des périodes allant de 5 à 50 ans (ces taux de rendement peuvent provenir de toute source de revenu périodique, que ce soit des intérêts, dividendes ou plus-values):
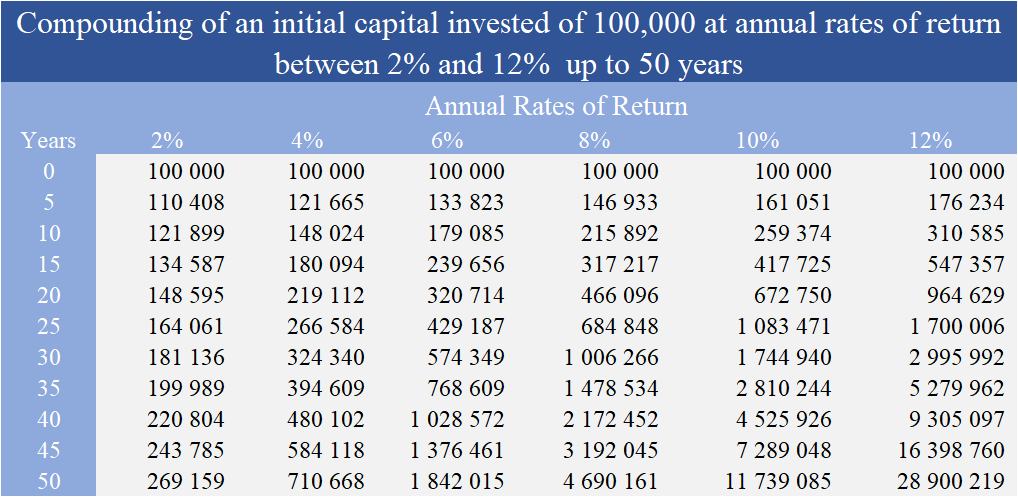
L’énorme augmentation de la puissance du rendement composé est parfaitement visible.
Après 10 années, le capital était évalué à plus de 2,5 fois à un taux de rendement annuel de 10% atteignant 259,374. Au bout de 20 ans, à ce rythme annuel, le le capital accumulé serait supérieur à 670 000 et au bout de 45 ans dépasserait 7,2 millions.
Même pour des taux de rendement inférieurs, l’effet du rendement composé est très important. Pour un taux de rendement de 6%, après 10 ans, le capital serait de 179,085, dépasser 320.000 à 20 ans et serait de 1,37 million au bout de 45 ans.
Ces périodes et ces taux de rendement sont réalistes et admissibles, et donc pas exagéré. L’horizon temporel de notre retraite dépasse 45 ans, ce qui correspond à la durée de notre vie active normale, 20 ans est un horizon pour l’éducation des enfants et 10 ans peuvent être la période pour acheter une maison ou la star de sa propre entreprise.
À la poste, sur les taux de rendement annuels moyens des principaux actifs nous avons vu que, de 1926 à nos jours, aux États-Unis, la moyenne était de 12%. taux de rendement annuel des actions des petites entreprises et 5% de celui des obligations à 10 ans Obligations du Trésor. Nous avons également vu que les taux de rendement annuels moyens des actions et les obligations n’étaient pas très différentes de ces valeurs.
Le graphique ci-dessous montre l’effet du rendement composé pour le même capital de départ de 100 000 et pour les taux annuels de rendement compris entre 2% et 10% sur un horizon de 40 ans:
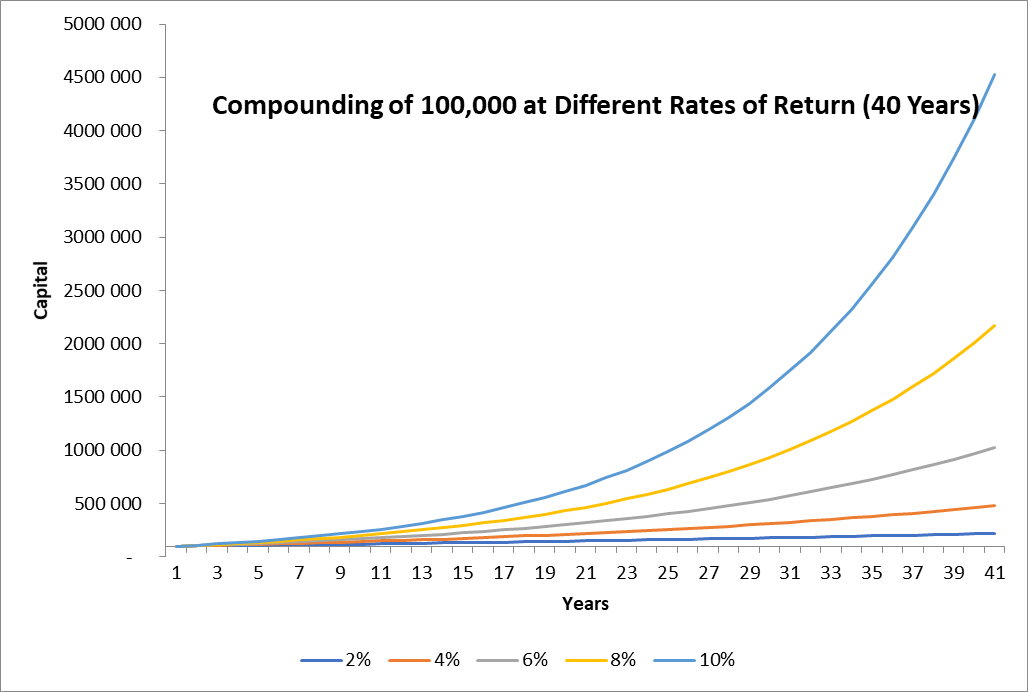
L’effet multiplicatif exponentiel est parfaitement visible sur le graphique.
Compound Interest Calculator | Investor.gov
La règle de 72 et nombre d’années pour doubler le capital
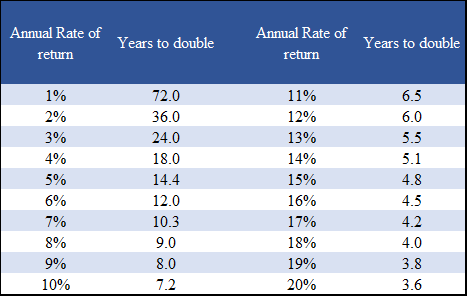
La “règle de 72 “est un simple ou une règle empirique, très utile pour obtenir le nombre de années nécessaires pour doubler le capital pour chaque valeur du taux de rendement. Cette règle nous donne une bonne approximation pour calculer rapidement le nombre d’années nécessaire pour doubler le capital:
Divisant 72 par taux annuel de retour donne le nombre d’années pour doubler le capital
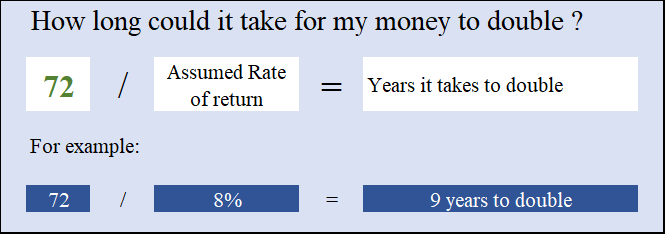
Exemples: 72/3% = 24 ans; 72/6% = 12 de les années; 72/12% = 6 ans; etc.
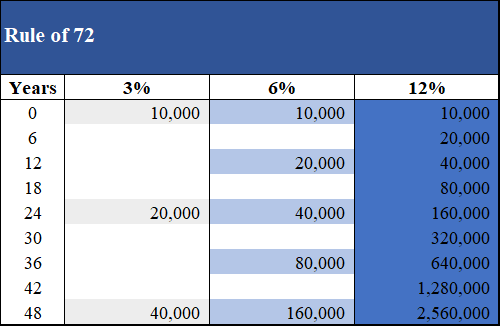
Si nous passons aux valeurs:
Avec 10 000 à 3% => 20 000 (24 années); => 40.000 (48 ans);
Avec 10 000 à 12% => 20 000 (6 années); => 40.000 (12 ans); => 160.000 (24 ans) => 2.560.000 (48 années)!
Le rendement composé est magique pour les investissements … mais implosive pour dettes
Le rendement composé est valable non seulement pour les investissements, mais également pour les dettes ou les emprunts, parce qu’il s’applique chaque fois qu’il y a des flux périodiques, qu’ils soient de revenus ou de coûts
Pour les investissements, nous avons un rendement composé positive. Le revenu travaille comme le “magie de la reproduction”. Est-ce comme “Sonic the Hedgehog” (le chiot nerveux) en finance. Nous avons des vents favorables qui nous poussent devant.
Mais pour les dettes ou les emprunts, nous avons l’inverse, le rendement composé négative. Les coûts augmenteront. Cela fonctionne comme “une spirale de dégénérescence”. C’est comme le “Pacman” (le mangeur) en finance. Nous avons des vents négatifs soufflant et nous tirant vers le bas.
Le rendement composé est à la fois l’émerveillement et le monstre (le “La belle et la Bête”)
Principales implications du rendement composé: payer les dettes et investir au plus vite
Être un facteur multiplicatif ou géométrique, et pas arithmétique, l’effet du rendement composé devient exponentiel.
C’est pourquoi nous devons vivre sans dettes. Si elles sont nécessaires (éducation, santé, etc.), nous devrions les rembourser dès que possible.
Pour cette raison, nous devons également réinvestir les revenus des investissements autant que possible. comme nous pouvons.
Le plus tôt vous commencez à investir mieux. Comme petit comme nous pouvons. Tout petit retard dans le présent signifie un effort accru dans le futur.