Interés compuesto o la Capitalización de intereses es la Octava Maravilla del mundo, el poderoso crecimiento del tiempo, la magia financiera y la regla del 72
La Octava Maravilla del mundo según Albert Einstein
La regla 72 y el número de años para duplicar el capital
El interés compuesto es mágico para las inversiones … pero implosivo por deudas
Principales implicaciones del interés compuesto: pagar deudas e invertir lo antes posible
La Octava Maravilla del mundo según Albert Einstein
Albert Einstein dijo una vez que: “El interés compuesto es la octava maravilla de la mundo; El que lo entiende, se lo gana; El que no, lo paga “.
¿Qué es el interés compuesto?
El capital invertido produce ingressos. Este ingreso puede reinvertirse conjuntamente con la capital. El ingreso producido por el ingreso por reinversión se llama interés compuesto. Para agravar, dado que los ingresos del capital se convierten en capital para inversión, produciéndose ingresos.
También se llama ingresos (ya sea intereses, dividendos, etc.). Es el ciclo de reproducción de la capital, como el ciclo de cría de animales o las plantas, en el que la descendencia se convierte en creador.
Como veremos, la capitalización de intereses tiene un poder exponencial para multiplicar el capital inicial invertido con el paso del tiempo. Einstein lo llamó la octava maravilla del mundo o la magia de las finanzas a este enorme poder de crecimiento de capital de hora.
La capitalización de intereses tiene un enorme poder exponencial para el crecimiento del capital con el tiempo
La siguiente tabla muestra el efecto de capitalización tomando como ejemplo un capital inicial invertido de 100.000 y varias tasas anuales de rendimiento, entre 2% y 12%, por períodos de 5 años hasta 50 años (estas tasas de rendimiento pueden provenir de cualquier fuente periódica de ingresos, ya sean intereses, dividendos o ganancias de capital):
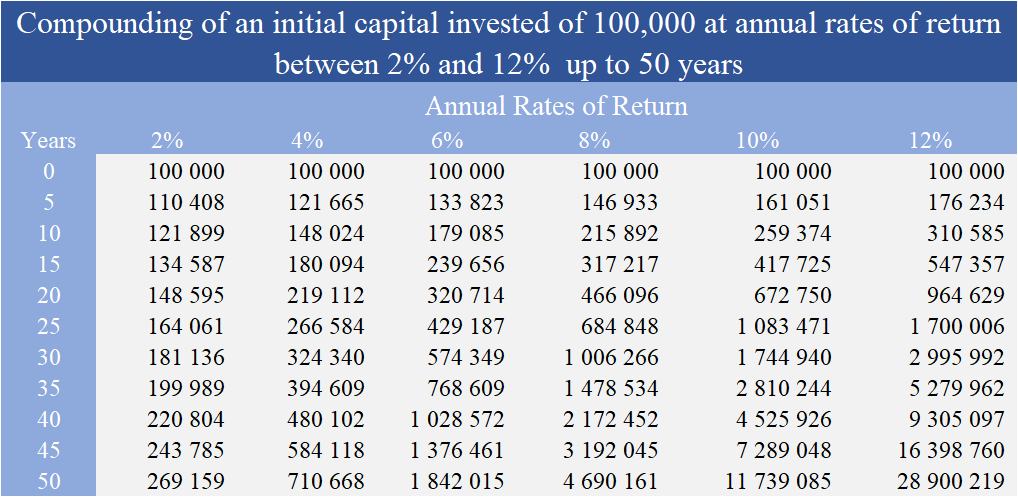
El enorme crecimiento de potencia de la capitalización es perfectamente visible.
Después de 10 años, el capital se valoró más de 2.5 veces a una tasa de rendimiento anual de 10% llegando a 259.374. Al final de 20 años, a esta tasa anual, el el capital acumulado sería mayor a 670,000 y al cabo de 45 años superaría los 7,2 millones.
Incluso para tasas de rendimiento más bajas, el efecto de capitalización es muy significativo. Para una tasa de rendimiento del 6%, después de 10 años el capital sería 179.085, sería excedería los 320,000 a los 20 años y sería de 1,37 millones al final de los 45 años.
Estos períodos y estas tasas de rendimiento son realistas y admisibles, y por lo tanto, no exagerado. El horizonte temporal de nuestra jubilación supera los 45 años, que es la duración de nuestro vida activa normal, 20 años es un horizonte para la educación universitaria de los niños y 10 años pueden ser el período para comprar una casa o la estrella de un negocio propio.
En la publicación sobre las tasas de retorno anual promedio de los principales activos vimos que en el período de 1926 a hoy, en los EE. UU., el 12% era el promedio tasa de rendimiento anual de acciones de pequeñas empresas y 5% la de bonos a 10 años Bonos del Tesoro. También vimos que las tasas anuales promedio de rendimiento de las acciones y los bonos no eran muy diferentes de estos valores.
El siguiente gráfico muestra el efecto de capitalización para el mismo capital inicial de 100.000 y para tasas anuales de retorno entre 2% y 10% para un horizonte temporal de 40 años:
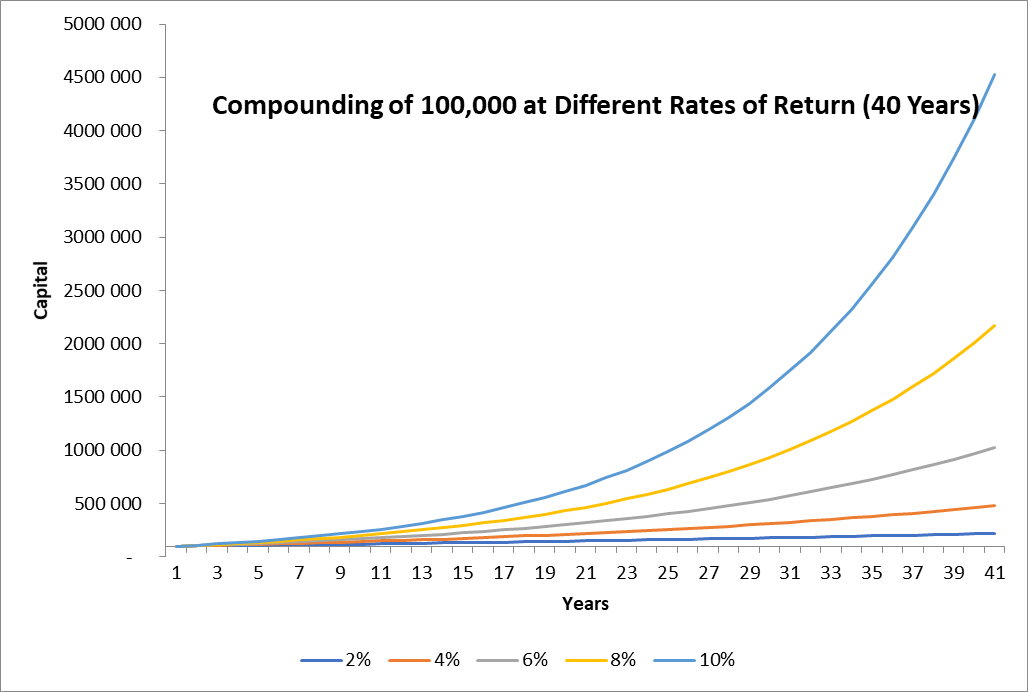
El efecto multiplicativo exponencial es perfectamente visible en el gráfico.
Compound Interest Calculator | Investor.gov
La regla de 72 y el número de años para duplicar el capital
La “regla de 72 “es una regla simple o práctica, muy útil para obtener el número de años necesarios para duplicar el capital por cada valor de la tasa de rendimiento. Esta la regla nos da una buena aproximación para calcular rápidamente la cantidad de años necesario duplicar el capital:
Dividiendo 72 por tasa anual de el retorno da el número de años para duplicar el capital
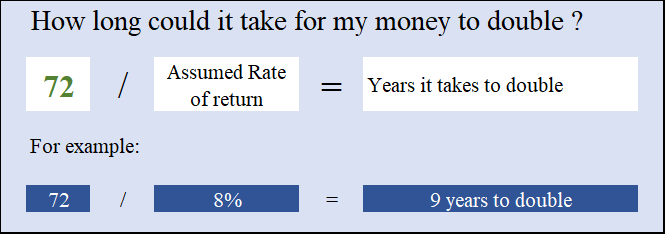
Ejemplos: 72/3% = 24 años; 72/6% = 12 de los años; 72/12% = 6 años; etc.
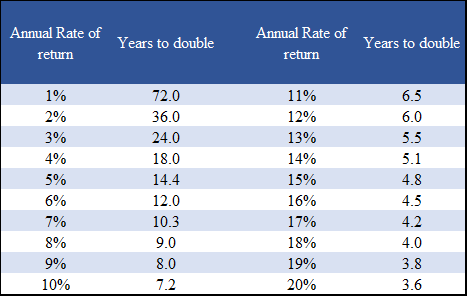
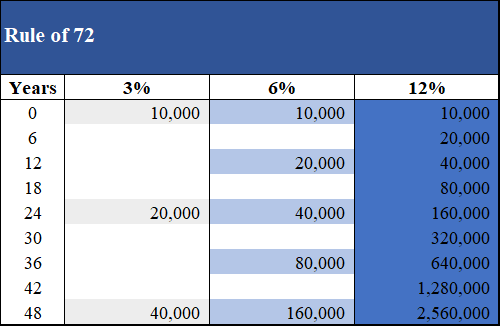
Si cambiamos a valores:
Con 10.000 a 3% => 20.000 (24 años); => 40,000 (48 años);
Con 10.000 a 12% => 20.000 (6 años); => 40.000 (12 años); => 160,000 (24 años) => 2,560,000 (48 años)!
La capitalización de intereses es mágica para las inversiones … pero implosiva para deudas
La capitalización es válida no solo para inversiones sino también para deudas o préstamos, porque se aplica siempre que haya flujos periódicos, ya sea de ingresos o costos.
Para las inversiones tenemos capitalización positiva. Los ingresos funcionan como el “Magia de reproducción”. Es como “Sonic the Hedgehog” (El cachorro nervioso) en las finanzas. Tenemos vientos favorables que nos soplan y empujan adelante.
Pero para las deudas o préstamos hacemos lo contrario, capitalización negativa. Los costos se incrementaran. Funciona como “una espiral de degeneración”. Es como el “Pacman” (el comedor) en finanzas. Tenemos vientos negativos que soplan y tirando de nosotros hacia abajo
La capitalización es simultáneamente la maravilla y el monstruo (el “La bella y la Bestia”)
Principales implicaciones de la capitalización de intereses: pagar deudas e invertir cuanto antes
Siendo un factor multiplicativo o geométrico, y no aritmética, el efecto de capitalización se vuelve exponencial.
Por eso debemos vivir sin deudas. Si son necesarios (educación, salud, etc.), debemos pagarlos tan pronto como podamos.
Por esta razón, también debemos reinvertir los ingresos de las inversiones tanto como podemos.
Cuanto antes comience a invertir mejor. Tan pequeño como podemos. Cualquier pequeño retraso en el presente significa un mayor esfuerzo en el futuro.