Compounding interest is the 8th Wonder of the World, the time powerful growth, financial magic, and the rule of 72
The 8th wonder of the World according to Albert Einstein
Compounding has a huge exponential power for capital growth with time
The 72 rule and the number of years to double the capital
Compounding is magical for investments… but implosive for debts
Main implications of compounding: pay debts and invest asap
The 8th Wonder of the world according to Albert Einstein
Albert Einstein once said that: “Compounding is the 8th wonder of the world; He who understands it, earns it; He who doesn’t, pays it.”
What is compounding of income or interest?
The capital invested produces income. This income can be reinvested jointly with the capital. The income produced by the reinvestment income is called compounding. Compounding, since the income of capital becomes capital for investment, producing itself income.
It is also called income compounding (whether interest, dividends, etc.). It is the reproduction cycle of the capital, such as the animal breeding cycle or the plants, in which the offspring becomes creator.
As we will see, compounding has an exponential power to multiply the initial capital invested with the passage of time. Einstein called it the 8th wonder of the World or the magic of finance to this enormous capital growth power of time.
Compounding has a huge exponential power for capital growth with time
The following table shows the compounding effect taking as an example an initial capital invested of 100.000 and several annual rates of return, between 2% and 12%, for 5 year periods up to 50 years (these rates of return may come from periodic any income source, whether interest, dividends or capital gains):
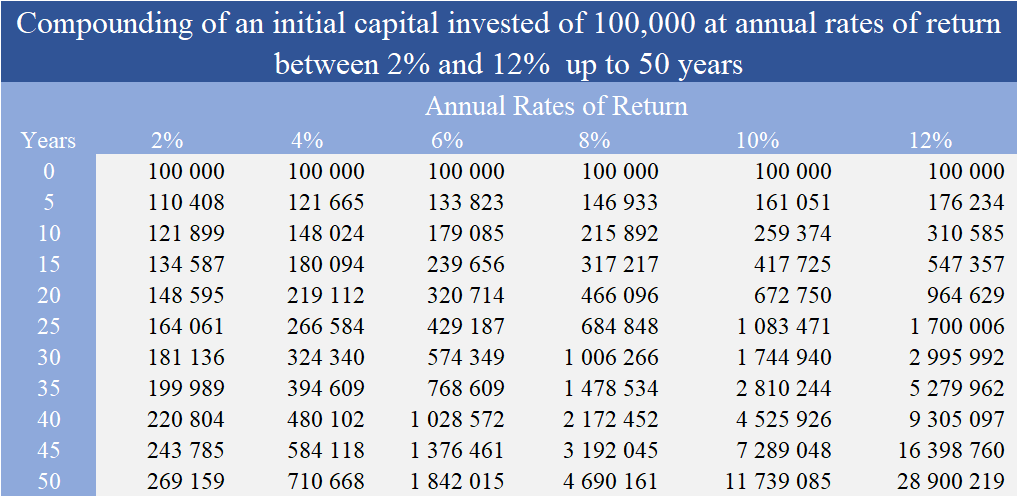
The enormous power growth of compounding is perfectly visible. After 10 years, capital was valued at more than 2.5 times at an annual return rate of 10% reaching 259.374. At the end of 20 years, at this annual rate, the accumulated capital would be greater than 670.000 and at the end of 45 years would exceed 7.2 million.
Even for lower rates of return the compounding effect is very significant. For a 6% rate of return, after 10 years the capital would be 179.085, would exceed 320.000 at 20 years and would be 1.37 million at the end of 45 years.
These periods and these rates of return are realistic and admissible, and therefore not exaggerated. The time horizon to our retirement exceeds 45 years, which is the duration of our normal active life, 20 years is a horizon for the children college education and 10 years can be the period to purchase a house or the star of own business.
In the post on the average annual return rates of the main assets we saw that in the period from 1926 to today, in the US, 12% was the average annual rate of return of small companies stocks and 5% the one for bonds of 10-year Treasury bonds. We also saw that the average annual rates of return for stocks and bonds were not very different from these values.
The following chart shows the compounding effect for the same starting capital of 100.000 and for annual rates of return between 2% and 10% for a time horizon of 40 years:
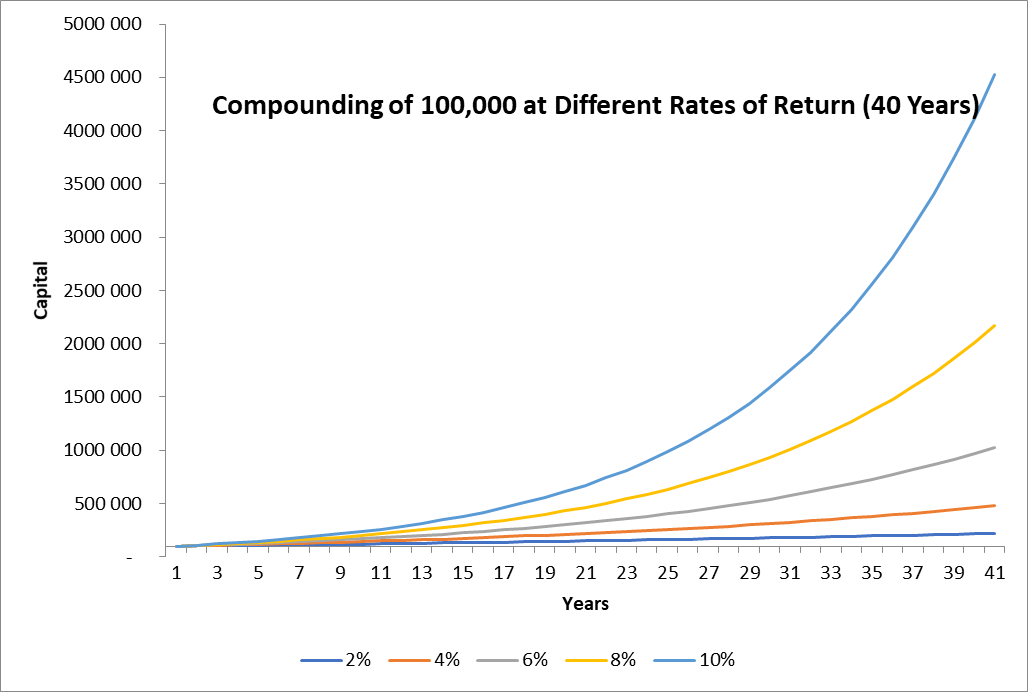
The exponential multiplicative effect is perfectly visible on the graph.
Compound Interest Calculator | Investor.gov
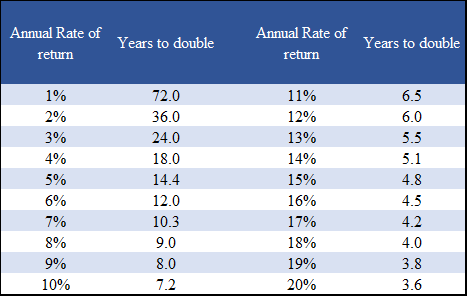
The rule of 72 and the number of years to double the capital
The “rule of 72” is a simple or rule of thumb, very useful for obtaining the number of years needed to double the capital for each value of the rate of return. This rule gives us a good approximation to quickly calculate the number of years needed to double the capital:
Dividing 72 per annual rate of return gives the number of years to double the capital
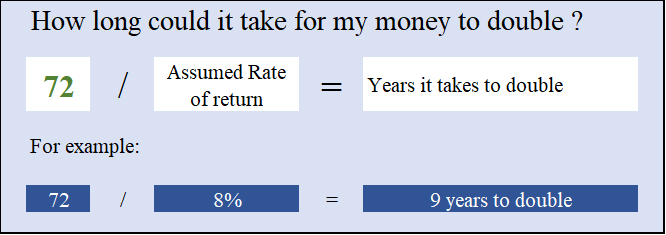
Examples: 72/3% = 24 years; 72/6% =12 of the years; 72/12% =6 years; etc.
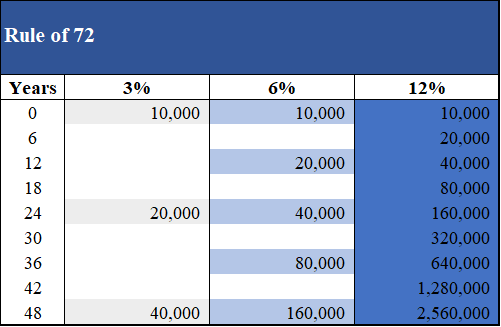
If we switch to values:
With 10.000 to 3% = > 20.000 (24 years); = > 40.000 (48 years);
With 10.000 to 12% = > 20.000 (6 years); = > 40.000 (12 years); = > 160.000 (24 years) = >2,560,000 (48 years)!
Compounding is magical for investments…but implosive to debts
Compounding is valid not only for investments but also for debts or loans, because it applies whenever there are periodic flows, whether of income or costs.
For investments we have positive compounding. Income is working as the “magic of reproduction”. Is the like “Sonic the Hedgehog” (the jumpy puppy) in finance. We have favorable winds blowing and pushing us ahead.
But for the debts or loans we the reverse, negative compounding. The costs will increase. It works out as “a degeneration spiral”. It is like the “Pacman” (the eater) in finance. We have negative winds blowing and pulling us down.
Compounding is simultaneously the wonder and the monster (the “Beauty and the Beast”)
Main implications of compounding: pay debts and invest asap
Being a multiplicative or geometric factor, and not arithmetic, the compounding effect becomes exponential.
That is why we must live without debts. If they are necessary (education, health, etc.), we should repay them as soon as we can.
For this reason, we also must reinvest the incomes of investments as much as we can.
The sooner you start investing better. As little as we can. Any small delay in the present means a greater effort in the future.